你有没有见到过这样的推文：中国有4亿中产阶级，人均月收入9000元！

前段时间在朋友圈看到各种个人纳税补交流程后有人喜有人忧，是不是感觉5000元都算小资了呢。

zui近又有新闻爆出："中国总资产已经达到了1302万亿元，人均资产约93万元。 我又拖国家的后腿了！

在朋友圈中，感觉每个人仿佛都是中产阶级，很多人都过着精致的小资生活，无论是在知乎还是抖音这些社交媒体平台，大家都在分享着自己光鲜的一面。 长久下来，知乎上好像遍地是高知，几乎每个回答的固定开头都是：“人在美国，刚下飞机，谢邀。”，抖音快手上晒吃晒喝的土豪视频刷都刷不完。 好像每个人都过得还不错，甚至有些人已经开始侃侃而谈中国什么时间能够超越美国，做全球的老大哥。 被平均已经很无奈，朋友圈又让你陷入小样本偏差。

我们都知道很多东西用平均去算是很愚蠢的，却深陷其中难以自拔：

每当被现实打脸：你醒醒，你还是个穷人！朋友圈都会过来安慰：看看，你的朋友们过得多滋润！ 直到总理的一句话把你彻底浇醒:我们的人均年收入是3万，但是有6亿人月均收入为1000。 不好意思，在你月入三千的你已经在平均线以上了。 你还不是穷人，只是有点穷。

除此之外，在生活中我们还有还有类似的错觉： 现在大学生不值钱了，遍地都是，本科生都不好找工作了，可现实是：“中国的本科率仅为4%” 其实我们这里说的平均数严格来说是算术平均数。 平均数*的缺陷是把差异给掩盖了，它无法告诉我们不同地区、不同行业、不同职位的工资差异。

不仅仅是收入，还有身高数据，2015年6月30日国务院新发布全国18岁及以上成年男性和女性的平均身高分别为167.1cm和155.8cm，平均体重分别为66.2kg和57.3kg。

你是不是又被平均了

就像某些段子调侃的：“张家有财一千万，九个邻居穷光蛋，平均起来算一算，个个都是张百万。”虽然*端，但它的确形象地反映了少量高收入人员的高工资，会把低收入者的收入水平给“拉起来”。人们感叹的“工资被增长”，也是反映了工资统计制度的这种缺陷。 既然平均数必须有，那就应该努力让它更接近真实。 过去，国家统计局发布的平均工资只统计了城镇非私营单位的工资，六七千万私营企业的职工看到那样的平均工资，难免心中苦涩。从2009年开始，统计局建立了私营单位工资统计调查制度。从当年公布的情况看，2008年底，占全国从业人员54.75%的城镇私营单位员工，平均工资只相当于此前统计的平均工资的58.4%。显然，有了这个数据，平均工资离人们的主观感受近了许多。 既然平均数有局限，那就应该给社会提供更多的数据。

2012年，国家统计局*公布了城乡居民收入的中位数。所谓中位数，就是一组数据中处于*中间的一个数据，它有助于了解普通民众的收入水平。比如，2011年城乡居民收入的中位数告诉我们，当年有一半的农村居民人均纯收入比平均数低783元，一半的城镇居民人均可支配收入比平均数低2692元。

显然，中位数剔除了*和*收入的影响，离大多数人对收入的真实感觉又近了一大步。

看下今年一季度人均收入的中位数和平均数的差异。

平均家族

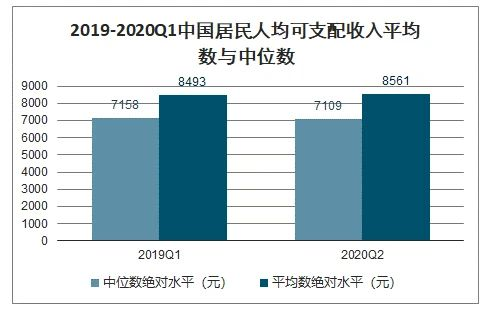
就像总理那句话的后半句：有6亿人月均收入为1000，我们对中位数的了解太晚了，才会让我们像个傻子似的被平均，却不知道真相。美国在上个世纪都已经开始使用中位数衡量国民可支配收入水平了。

其实很多事情，现实早有佐证，比如拼多多之所以快速崛起，不正好说明了中国还有很多“五环之外”的人吗，存在即合理。

4亿人都在用，这就是事实。

还有*近被激活的地摊经济，几天之间，大街小巷满是地摊，除了少数作秀的，大部分人还真是为了挣口生活费，有钱谁摆摊，事实总不会骗人吧。

做金融风险管理的，在投资领域要经常面对市场上的各种数据，尤其是对投资影响较大的几个：GDP增长率、失业率、CPI、PPI。这些数据的正确性与否及对其解读是否正确直接决定了投资的成败。

这不，前两天米国还闹出了大乌龙。

上周五米股大涨，原因是本来市场预期5月米国减少750万就业，结果统计局数据是增加了250万。相当于突然有1000万人找到了工作，直接震撼了股市。

这事不太好解释，因为目前美联储预期2季度GDP腰斩，就业不减少也就算了，怎么可能突然多出来呢？

被市场打爆的空头们打爆了米国统计局的电话，*终结果是统计局承认有乌龙。大致原因是：调查表格中有一项“因为其他原因没有上班”，正常数据大约是50万左右。这一项的意思是大概是主动失业，类似于家里有矿的，明明可以找到工作但每年躺赚30万懒得去。所以这些人是不被算为失业的。

但由于米国群众误解了这个“其他原因”，认为疫情也属于“其他原因”，所以5月有540万人选择这个选项。差额的490万基本就是实际上没工作但被算成财务自由的。

不过米国统计局说了，虽然这一项很可能是乌龙，但填都填了无法更正。你们就当做还是新增250万好了，至于以后调查中是不是进行调整再说。

数据可能会出错，逻辑不能出错，对各种统计数据要的深入的理解，这也是对一个投资风险管理者的基本素养。

上面都是开胃菜，在金融领域还有三个金刚：几何平均数、调和平均数、加权平均数。

看清投资业绩的利器：几何平均数！

举个栗子：

如果你是一个基金经理，管理着一支基金，规模是100万元，今年行情好，到年底的时候涨到了200万元；然而第二年行情很差，又跌回了100万元，请问这支基金在这两年内的平均收益率是多少？

我们分开计算：*年的收益率=（200-100）/100=100%；*年的收益率是100%，盈利；第二年的收益率=（100-200）/200=-50%；第二年的收益率是-50%，亏损；

那么平均收益率该怎么算呢，一般人可能会把这两个收益率加起来除以二：[100%+（-50%）]/2=25%；

也就是说平均收益率有25%，基友一看，那好，你基金经理把25%的收益率给我，我投了100万，你把25万给我。

你一看，期初管理了100万的基金规模，两年后还是100万的基金规模，并没有多出的25万给基友啊，那这平均收益率难道错了吗？

其实不是平均收益率错了，而是你选用计算平均收益率的方式错了。

这里我们不能用算术平均数的方法计算，而应该用几何平均数的方法计算：

（1+r）（1+r）=(1+100%)(1-50%)； r=0；

为啥呢

算术平均数使用的前提条件是每个数据之间不具有相互影响关系，是独立存在的。

而几何平均数适用的场景则是，每个数据之间是相互影响的，后一个数据是建立在前一个数据之上的，是一种相乘的关系，投资中连续几年的收益率恰恰是符合这样的条件。

现实中有一些无良投资管理公司就是拿算术平均法来计算投资业绩的，注意擦亮眼睛。

定投平摊成本的奥秘：调和平均数！

很多人在定投时，会过多关注收益率。但其实评估定投效果，更核心的是考量定投对平均成本的影响。在定投过程中，成本到底是如何被平摊的，真的是算术平均这么简单吗？

*，通常我们用来衡量基金定投的成本会用到调和平均数。

调和平均数的计算公式：

平均家族

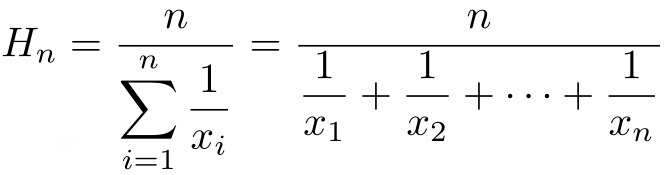
举个栗子：

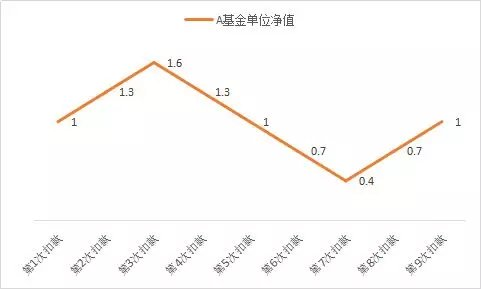
震荡的市场中，A基金单位净值走势如表格1所示，在这个过程中，通过基金定投完成了9次扣款，假设每次定投100元，*终的定投成本是多少（忽略费用）？初看上去，定投在高处的次数与定投在低处的次数很平均，*终平均下来的成本应该和*终的基金净值“1”差不离？

平均家族

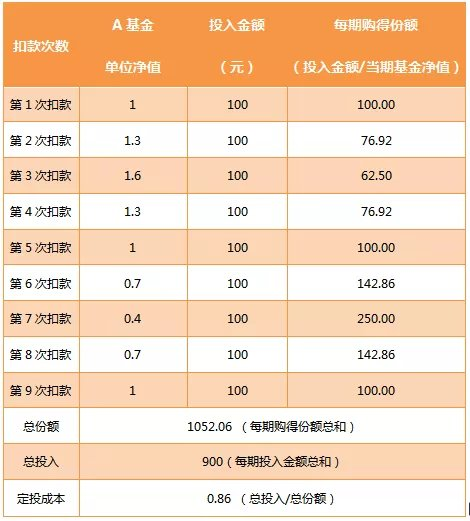
我们用计算来检验一下这种想法吧。如表格2所示，经过9次扣款获得的总份额为1052.06份、总投入为900元，计算得每一份额基金的定投成本为“0.86”，低于此时基金的单位净值“1”，意味着已经盈利！

平均家族

套用前文所说的“调和平均数”计算公式，本题中定投成本的计算过程其实是：

平均家族

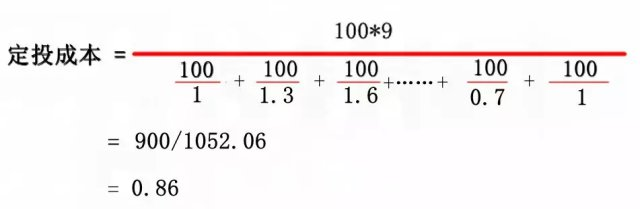
定投成本=总投入/总份额，因为每期的投入固定，定投的总投入是确定的，影响*终结果的关键，在于因每次买入“单价（基金单位净值）”不同而带来的份额变化：如果基金净值越低，买到的份额越多，*终相同的钱买到的总份额越多、定投成本就越低。

在本案例中，基金净值位于低谷时所执行的扣款，对*终成本的降低起到了重要作用，尤其是第7次扣款时基金净值低至0.4，买入份额高达250份，*大地平摊了成本！这也恰好说明了“为什么市场回调时不能中止定投”，因为万一这样做了，定投平摊成本的效果就会大打折扣。

调和平均数的应用条件：调和平均数可以用在相同距离但速度不同或相同时间但对应的数值不同时，平均值的计算。而基金定投恰恰符合这样的场景。

调和平均数的缺点：

①调和平均数易受*端值的影响，且受*小值的影响比受*大值的影响更大。②只要有一个标志值为0，就不能计算调和平均数。

投资组合的平均收益率：加权平均数！

直接上例子：假如有一个基金经理管理了一个基金，里面有两只股票A股票B，其中股票A仓位比重是40%,股票B的仓位比重是60%,股票A今年的收益率为5%，另一只B的今年的收益率为12%，那么这个基金平均收益了是多少？

这个例子中其实只有两个数值，只不过每个数值自带权重，这个时候就要用到加权平均数了，直接带入加权平均数的计算公式。

基金平均收益率=40%×5%+60%×12%=7.4%。

凡是数值自带权重的，就要考虑到加权平均数了。除了投资管理领域外，在商品进货平均核算和销售毛利率核算方面，加权平均数也是独领风骚。

比如，你是一个水果店的老板，只卖两种水果，苹果和香蕉，苹果进价一公斤5块，卖7块；香蕉进价一公斤8块，卖10块；一般苹果进货占比7成，香蕉进货占比3成。

那么水果店的平均进货成本就是：5×0.7+8×0.3=5.9元.平均毛利就是：（7-5）/7×0.7+（10-8）/10×0.3=26%.

小老板们赶紧学习下吧。

平均家族里常用的五位成员，都是随着时代的进步应运而生，每个人都有擅长的领域，如果用错了，闹笑话事小，亏钱事大。