想在金融界有一番作为，肯定是需要拿出看见本领的，首先，你就是需要有进入金融界的敲门砖——FRM证书。下文是对FRM刻画随机变量—FRM一元分布函数的介绍，送给备考的你。

经典的概率方法基于随机变量（random variable，RV）。例如，在掷骰子时，每一个结果由一个固定过程产生，如果骰子是*对称的，我们可以认为在一次投掷中观察到一次6点的概率为p=1/6，虽然事件本身是随机的，但我们仍然可以从一个固定的数据产生过程中得到许多有用的结论。

同样的方法可以用于金融市场，这里的股票价格、汇率、收益率和大宗商品价格均可视为随机变量。但与上述实验相比，这些随机变量的固定数据产生过程的假设条件更弱一些。

>>>点击领取2020FRM备考资料大礼包（戳我领取）

FRM一元分布函数：

一个随机变量X用一个分布函数（distribution function）刻画：F（x）=P（X≤x），它是随机变量X的真实结果小于等于给定的数x的概率，这也被称为累积分布函数（Cumulative distribution function）。

当随机变量X取值离散值时，这个分布由小于等于x的概率直接加总得到，即：

FRM一元分布函数

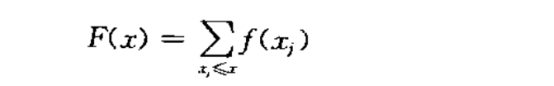
这里，函数f（x）称为频率函数（Frequency function），或者是概率密度函数（Probability density function，PDF）。

当随机变量连续时，分布为：

FRM一元分布函数

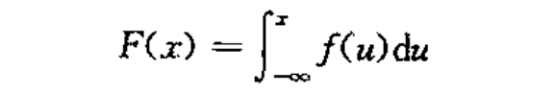
密度函数可以由分布函数得到：

FRM一元分布函数

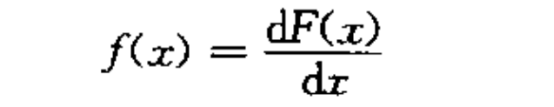
通常，分布函数或者密度函数可以等同地对随机变量进行描述。

这些函数具有显着的性质，密度函数f（u）对于所有的u必须为正。当x趋于无穷时，分布趋于1，因为它代表x的任意抽样的总概率：

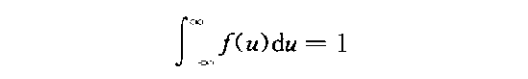
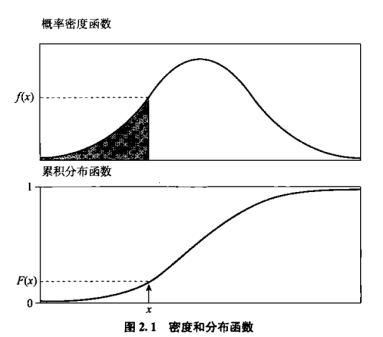
FRM一元分布函数

FRM一元分布函数

上图中上部给了密度函数f（x）的一个例子，下部是累积分布函数F（x）的一个例子。F（x）度量f（x）曲线与x轴之间的小于等于x的面积，用阴影部分表示。这里，这个面积为0.24，对于很小的x，F（x）接近于0，相反地，对于很大的x，F（x）接近于1。