金融知识差对FRM考生来说，是一个挑战。下文为考生介绍一下FRM构建投资组合的内容，希望对备考FRM的你有帮助！

FRM构建投资组合主要有：多种资产比较、风险调整业绩度量、混合资产、有效边界。下面为大家详细说下FRM风险调整业绩度量。

首先是如何用一个单独风险度量来调整业绩。同样的方法可应用于过去或者未来的业绩调整，过去的业绩调整要用到历史平均业绩值，未来的业绩调整要用到预测的数值。

*简单的度量是夏普比率（Sharpe ratio，SR），它是平均收益率μ（Rp）超过无风险收益率Rp的部分与*风险的比率：

SR=[μ(Rp)-Rp]/σ(Rp)

夏普比率重点考虑以*形式度量的总体风险。这种方法可以扩展到将VAR或者收益率的分位数作为分母代替收益率的波动率。

下图比较了两种投资工具的夏普比率。假设我们拥有一种无风险资产，现金，收益率3%。夏普比率是从现金到每一种资产的直线的斜率。该直线代表现金和每一种资产的投资组合。在这个例子中，股票的夏普比率比债券大。这意味着在相同的波动率下，选择现金和股票的投资组合比现金和债券的投资组合具有更高的收益率。

比较夏普比率

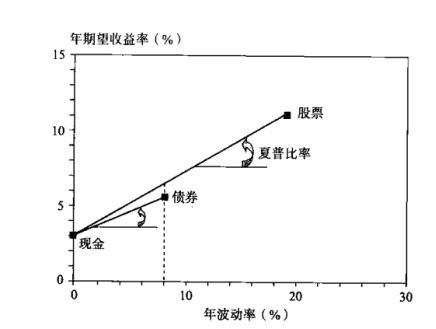
比较夏普比率

这可以推广到相对风险度量上。信息比率（information ratio，IR）度量了平均收益率P超过基准收益率B的部分与TEV之间的比率：

IR=[μ(Rp)-μ(RB)]/σ(Rp-RB)

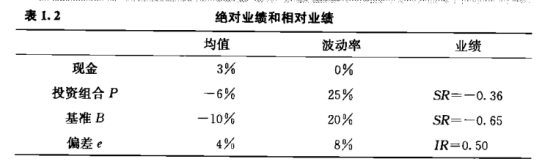
上表做了一个说明。无风险利率为RF=3%，投资组合的平均收益率为-6%，波动率为25%。因此，投资组合的夏普比率为SR=[(-6%)-(3%)]/25%=-0.36。由于这是个负值，因此*业绩很差。

假设现在同时期的基准收益率为-10%并且追踪误差波动率为8%。因此，信息比率IR=[(-6%)-(-10%)]/8%=0.50，这是个正值。相对业绩*，即使*业绩很差。

追踪误差波动率可以从投资组合收益率和基准收益率的波动率σp和σB以及它们的相关系数ρ得到。随机变量之和的方差可以用各个随机变量方差之和加上两倍的协方差项来表示。那么偏差的方差为：

ω^2=σp^2-2ρσpσB+σB^2

例如，如果σp=25%，σB=20%，ρ=0.961，我们有ω^2=25%^2-2*0.961*25%*20%+20%^2=0.0064，得到ω=8%。

>>>点击领取：各科必背定义+历年真题中文解析+学习备考资料（PDF版）

学习备考资料

信息比率的一个缺点是TEV无法对平均收益率进行调整。例如，投资组合可能系统性地超过它的基准每月0.10%。在这种情况下，追踪误差的均值为0.10%并且标准差接近于零。这导致产生一个*高的信息比率，在主动型风险无法轻易度量的情况下这个结果并不真实。