在FRM考试中,几何平均数是对各变量值的连乘积开项数次方根。求几何平均数的方法叫做几何平均法。那么,它的特点是什么?>>>点击领取2020FRM备考资料大礼包(戳我免·费领取)
几何平均数是n个变量值连乘积的n次方根。分为简单几何平均数与加权几何平均数。
![]()
几何平均数特点:【资料下载】点击下载[Kaplan]FRM 2020 SchweserNotes Part I
1、几何平均数受ji端值的影响较算术平均数小;
2、如果变量值有负值,计算出的几何平均数就会成为负数或虚数;
3、它仅适用于具有等比或近似等比关系的数据;
4、几何平均数的对数是各变量值对数的算术平均数。
几何平均数应用:
例:假定某地储蓄年利率(按复利计算):5%持续1.5年,3%持续2.5年,2.2%持续1年。求此5年内该地平均储蓄年利率。
解:由
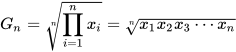
得到该地平均储蓄年利率:
![]()
几何平均数主要用途:
1、对比率、指数等进行平均;
2、计算平均发展速度;
其中:样本数据非负,主要用于对数正态分布。
3、复利下的平均年利率;
4、连续作业的车间求产品的平均合格率。
本文章为学习相关信息展示文章,非课程及服务内容文章,产品及服务详情可咨询网站客服微信。
文章转载须注明来源,文章素材来源于网络,若侵权请与我们联系,我们将及时处理。
金融风险管理师FRM考试百科
证书星级
- 报考条件
- 报名时间
- 报名费用
- 考试科目
- 考试时间
-
GARP对于FRM报考条件的规定:
What qualifications do I need to register for the FRM Program?
There are no educational or professional prerequisites needed toregister.
翻译为:报名FRM考试没有任何学历或专业的先决条件。
可以理解为,报名FRM考试没有任何的学历和专业的要求,只要是你想考,都可以报名的。查看完整内容 -
2024年5月FRM考试报名时间为:
早鸟价报名阶段:2023年12月1日-2024年1月31日。
标准价报名阶段:2024年2月1日-2024年3月31日。2024年8月FRM考试报名时间为:
早鸟价报名阶段:2024年3月1日-2024年4月30日。
标准价报名阶段:2024年5月1日-2024年6月30日。2024年11月FRM考试报名时间为:
早鸟价报名时间:2024年5月1日-2024年7月31日。
标准价报名时间:2024年8月1日-2024年9月30日。查看完整内容 -
2023年GARP协会对FRM的各级考试报名的费用作出了修改:将原先早报阶段考试费从$550上涨至$600,标准阶段考试费从$750上涨至$800。费用分为:
注册费:$ 400 USD;
考试费:$ 600 USD(第一阶段)or $ 800 USD(第二阶段);
场地费:$ 40 USD(大陆考生每次参加FRM考试都需缴纳场地费);
数据费:$ 10 USD(只收取一次);
首次注册的考生费用为(注册费 + 考试费 + 场地费 + 数据费)= $1050 or $1250 USD。
非首次注册的考生费用为(考试费 + 场地费) = $640 or $840 USD。查看完整内容 -
FRM考试共两级,FRM一级四门科目,FRM二级六门科目;具体科目及占比如下:
FRM一级(共四门科目)
1、Foundations of Risk Management风险管理基础(大约占20%)
2、Quantitative Analysis数量分析(大约占20%)
3、Valuation and Risk Models估值与风险建模(大约占30%)
4、Financial Markets and Products金融市场与金融产品(大约占30%)
FRM二级(共六门科目)
1、Market Risk Measurement and Management市场风险管理与测量(大约占20%)
2、Credit Risk Measurement and Management信用风险管理与测量(大约占20%)
3、Operational and Integrated Risk Management操作及综合风险管理(大约占20%)
4、Liquidity and Treasury Risk Measurement and Management 流动性风险管理(大约占15%)
5、Risk Management and Investment Management投资风险管理(大约占15%)
6、Current Issues in Financial Markets金融市场前沿话题(大约占10%)查看完整内容 -
2024年FRM考试时间安排如下:
FRM一级考试:
2024年5月4日-5月17日;
2024年8月3日(周六)上午;
2024年11月2日-11月15日。FRM二级考试:
2024年5月18日-5月24日;
2024年8月3月(周六)下午;
2024年11月16日-11月22日。查看完整内容
-
中文名
金融风险管理师
-
持证人数
25000(中国)
-
外文名
FRM(Financial Risk Manager)
-
考试等级
FRM考试共分为两级考试
-
考试时间
5月、8月、11月
-
报名时间
5月考试(12月1日-3月31日)
8月考试(3月1日-6月30日)
11月考试(5月1日-9月30日)










