期权和衍生品估值通常被认为是一个很困难的方面，通常需要物理学博士的数学水平。但是通过数值方法应用这些模型没有那么困难，比理论模型要简单一些。

对于欧式行权的期权来说，这种简单性更为明显。所谓欧式行权，指的就是在某个确定的日期行权。对于美式的期权来说，可以在一段时间内行权，会变得更为困难一些。今天融跃小编就如何使用Monte Carlo模拟进行复杂衍生品的定价：

随机过程在量化金融中的*应用是衍生品定价。当对衍生品进行定价时，大多数量子将使用两种方法中的一种。他们要么为他们定价的衍生物解决（或找到解决方案）Black Scholes模型，要么他们将使用模拟方法来估计导数的值。这两种技术都严重依赖于使用随机过程来模拟底层证券。

衍生定价方法一 Black Schole

Black Scholes模型用于在一组假设下对特定类型的衍生品合约进行定价。这些假设包括：

（1）存在无风险利率，任何金额可以借入或借出，

（2）基础价格根据几何布朗运动随机过程（稍后讨论），

（3）进化基础不支付股息，

（4）市场上没有套利机会，

（5）市场无摩擦意味着交易成本为零，

（6）可以买入或减去任何数量的潜在的。

在这些假设下，可以导出着名的Black Scholes偏微分方程。

Python

Black Scholes公式以及各种封闭形式期权定价公式的推导，是过去三十年中衍生品交易所大量增长的主要原因。

导数定价方法二 - 模拟方法

鉴于Black Scholes公式隐含的局限性和假设，通常采用蒙特卡罗方法（模拟）来为更少的简化假设。

这两个选项在计算复杂性和时间之间进行权衡。每次想要对导数进行定价时，使用模拟方法计算复杂度更高，但是为替代随机过程推导Black Scholes偏微分方程的“等价”更加耗时，然后仍然找到封闭形式的衍生品定价式。因此，大多数量子使用模拟方法。

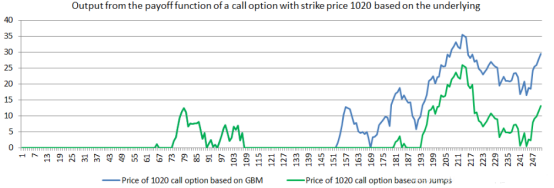
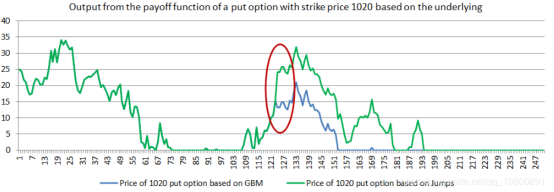
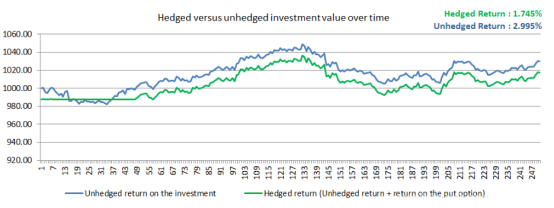
想要这样做的原因如下图所示。事实上，你如何选择和校准你的随机过程将对期权的预期收益产生重大影响，因此它的价值也是如此。

Python

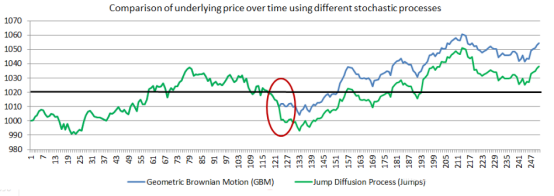
红色椭圆形显示市场跳跃的位置 。

Python

Python

使用衍生工具进行套期保值

套期保值是风险管理战略，旨在减少的量可对冲风险的投资组合暴露。可对冲风险包括股票风险，利率风险，货币风险，信用风险，波动风险和商品风险。套期保值是通过投资与投资组合中的基础负相关的资产来完成的。*简单的例子是在股票上买入看跌期权。当股票表现不佳时，看跌期权表现良好，而整体投资组合并没有像没有对冲时那样糟糕。净效应是抑制回报或下降。

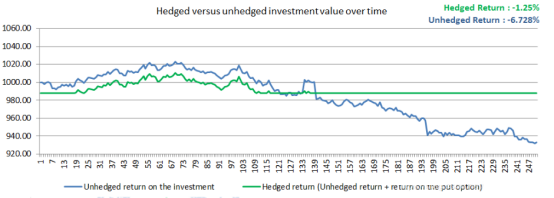
Python

Python

公司和基金将尝试确定投资组合所面临的风险因素并对冲这些风险因素。